What Is Sin 45 Apex

The value of sin 30 degrees is 0.5. Sin 30 is besides written as sin π/6, in radians. The trigonometric function besides called as an angle role relates the angles of a triangle to the length of its sides. Trigonometric functions are important, in the study of periodic phenomena similar audio and light waves, average temperature variations and the position and velocity of harmonic oscillators and many other applications. The most familiar three trigonometric ratios are sine office, cosine role and tangent function.

For angles less than a right angle, trigonometric functions are commonly defined as the ratio of two sides of a right triangle. The angles are calculated with respect to sin, cos and tan functions. Unremarkably, the degrees are considered equally 0°, 30°, 45°, 60°, 90°, 180°, 270° and 360°. Here, we will discuss the value for sin 30 degrees and how to derive the sin 30 value using other degrees or radians.

Sine xxx Degrees Value

The exact value of sin 30 degrees is ½. To define the sine function of an angle, showtime with a correct-angled triangle ABC with the bending of involvement and the sides of a triangle. The 3 sides of the triangle are given equally follows:

The opposite side is the side opposite to the angle of interest.
The hypotenuse side is the side opposite the right angle and it is ever the longest side of a right triangle
The adjacent side is the side adjacent to the bending of interest other than the right angle

The sine function of an bending is equal to the length of the opposite side divided past the length of the hypotenuse side and the formula is given by:

\(\begin{array}{l}\sin \theta =\frac{contrary ~ side}{hypotenuse ~ side}\end{array} \)

Sine Law: The sine law states that the sides of a triangle are proportional to the sine of the opposite angles.

\(\begin{assortment}{l}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\end{array} \)

The sine rule is used in the post-obit cases :

Case 1: Given 2 angles and i side (AAS and ASA)

Case 2: Given two sides and not included angle (SSA)

The other of import sine values with respect to bending in a right-angled triangle are:

Sin 0 = 0

Sin 45 = 1/√2

Sin lx = √3/2

Sin ninety = ane

Fact: The values sin 30 and cos 60 are equal.

Sin thirty = Cos 60 = ½

And

Cosec 30 = i/Sin xxx

Cosec thirty = 1/(½)

Cosec 30 = 2

Derivation to Observe the Sin 30 value (Geometrically)

Let us now calculate the sin 30 value. Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore

\(\begin{assortment}{fifty}\angle A=\bending B=\bending C=threescore^{\circ}\end{array} \)

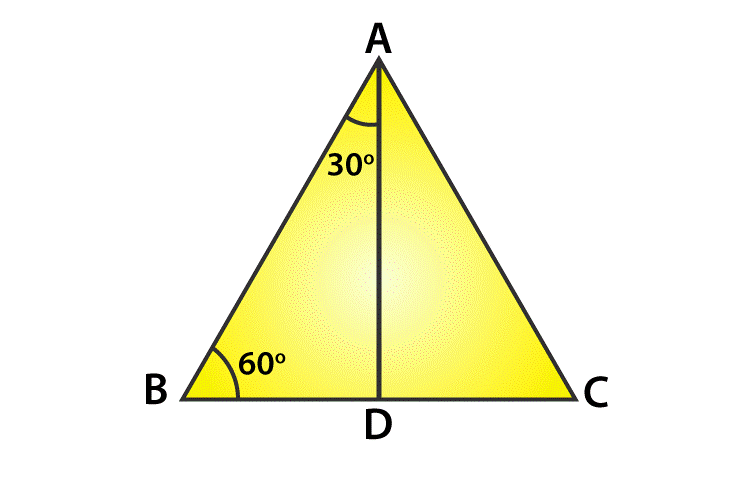
sin 30 degrees

Describe the perpendicular line AD from A to the side BC (From figure)

\(\begin{array}{fifty}Now \ \Delta ABD\cong \Delta ACD\end{array} \)

Therefore BD=DC and also

\(\brainstorm{assortment}{l}\bending BAD=\bending CAD\end{array} \)

Now notice that the triangle ABD is a right triangle, correct-angled at D with ∠BAD = thirty° and ∠ABD = 60°.

As you know, for finding the trigonometric ratios, we need to know the lengths of the sides of the triangle. And so, let usa suppose that AB=2a

\(\brainstorm{array}{l}BD=\frac{i}{2}BC=a\terminate{array} \)

To notice the sin thirty-degree value, let's utilize sin 30-degree formula and it is written every bit:

Sin xxx° = opposite side/hypotenuse side

We know that, Sin 30° = BD/AB = a/2a = i / two

Therefore, Sin 30 degree equals to the fractional value of 1/ 2.

Sin 30° = 1 / ii

Therefore, sin 30 value is 1/ii

In the same way, we can derive other values of sin degrees like 0°, 30°, 45°, 60°, ninety°,180°, 270° and 360°. Below is the trigonometry tabular array, which defines all the values of sine along with other trigonometric ratios.

Why Sin 30 is equal to Sin 150

The value of sin 30 degrees and sin 150 degrees are equal.

Sin 30 = sin 150 = ½

Both are equal considering the reference angle for 150 is equal to xxx for the triangle formed in the unit of measurement circumvolve. The reference angle is formed when the perpendicular is dropped from the unit circle to the x-axis, which forms a right triangle.

Since, the angle 150 degrees lies on the IInd quadrant, therefore the value of sin 150 is positive.The internal angle of triangle is 180 – 150=30, which is the reference angle.

The value of sine in other 2 quadrants, i.east. third and 4th are negative.

In the same fashion,

Sin 0 = sin 180

Trigonometry Table

Trigonometry Ratio Table
Angles (In Degrees)	0	30	45	60	90	180	270	360
Angles (In Radians)	0	π/6	π/four	π/3	π/two	π	3π/2	2π
sin	0	i/2	ane/√2	√3/2	1	0	−1	0
cos	1	√3/two	1/√2	one/2	0	−1	0	1
tan	0	1/√3	1	√3	Not Divers	0	Not Defined	0
cot	Not Defined	√3	one	one/√three	0	Not Defined	0	Not Divers
cosec	Not Divers	two	√ii	2/√3	1	Not Defined	−1	Not Divers
sec	i	2/√3	√ii	2	Not Defined	−one	Non Defined	1

Solved Examples

Question i: In triangle ABC, correct-angled at B, AB = 5 cm and angle ACB = 30°. Determine the length of the side AC.

sin 30 degrees 1

Solution:

To detect the length of the side Air-conditioning, we consider the sine part, and the formula is given by

Sin 30°= Reverse Side / Hypotenuse side

Sin 30°= AB / Air conditioning

Substitute the sin thirty value and AB value,

\(\begin{array}{l}\frac{1}{2}=\frac{v}{AC}\cease{array} \)

Therefore, the length of the hypotenuse side, Air conditioning = 10 cm.

Question 2: If a right-angled triangle has a side opposite to an angle A, of 6cm and hypotenuse of 12cm. And so find the value of bending.

Solution: Given, Side opposite to angle A = 6cm

Hypotenuse = 12cm

By sin formula nosotros know that;

Sin A = Opposite side to angle A/Hypotenuse

Sin A = 6/12 = ½

We know, Sin thirty = ½

So if we compare,

Sin A = Sin 30

A = xxx

Hence, the required bending is 30 degrees.

Question three: If a right-angled triangle is having side by side side equal to 10 cm and the measure of angle is 45 degrees. Then detect the value hypotenuse of the triangle.

Solution: Given next side = 10cm

We know,

Tan 45 = Opposite side/Next side

Tan 45 = opposite side/ten

Since, Tan 45 = one

Therefore,

1 = Opposite side/10

Opposite side = x cm

Now, past sin formula, nosotros know,

Sin A = Opposite side/Hypotenuse

So,

Sin 45 = 10/Hypotenuse

Hypotenuse = 10/sin 45

Hypotenuse = 10/(1/√2)

Hypotenuse = 10√2

Keep visiting BYJU'S for more information on trigonometric ratios and its related articles, and also watch the videos to analyze the doubts.

Frequently Asked Questions – FAQs

What is the exact value of sine 30 degrees?

The exact value of sin xxx degrees is 0.5.

What is the value of sine 30 in the class of fraction?

The value of sin 30 in the course fraction is ½

What is sine 30 degrees in radian?

Sine 30 degrees in radian is given by sin π/half dozen.

What is the formula for sine role?

Sine of an bending, in a right-angled triangle, is equal to the ratio of contrary side of the angle and hypotenuse.
Sine A = Contrary Side/Hypotenuse

What is the value of cos thirty and tan 30?

The value of cos 30 degrees is √three/2 and the value of tan xxx degrees is 1/√3.

How to discover the value of tan thirty with respect to sin and cos?

Tangent of an angle is equal to the ratio of sine and cosine of the same angle. Therefore,
Tan 30 = sin thirty/cos 30
Nosotros know that, sin thirty = ½ and cos 30 = √3/2
Therefore, tan 30 = (½)/√three/2
Tan thirty = 1/√iii